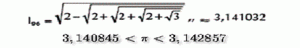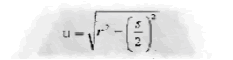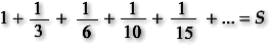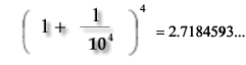Los SÍmbolos Secretos de los Rosa Cruces de los s.XVI y XVII

Los Simbolos Secretos de Los Rosa Cruces de Los s.xvi y XVII

Johannes Kepler: Harmonices Mundi

JOHANNES KEPLER:

HARMONICES MUNDI

Harmonices Mundi (La Armonía de los Mundos, 1619) es un libro escrito por Johannes Kepler en la ciudad de Linz. El libro contiene la primera formulación de la tercera ley del movimiento planetario.

En Harmonices mundi Kepler intenta explicar los movimientos planetarios con base en un modelo geométrico de proporciones entre diferentes poliedros relacionando éstos con escalas musicales. En esta obra muestra sus intentos de fijar las órbitas de los planetas en el interior de poliedros perfectos o sólidos platónicos tal y como había hecho en una obra anterior Misterium Cosmographicum. Para su gran decepción la teoría nunca funcionó y tras haberla expuesto en largas páginas en esta obra la abandona finalmente mostrando que es incompatible con las observaciones y las leyes del movimiento planetario deducidas por el en Astronomía Nova y Harmonices Mundi. Kepler intentó describir estos movimientos postulando una fuerza similar al magnetismo que él pensaba emanaba del Sol.

Kepler expuso en esta obra su teoría de que cada planeta produce un tono musical durante su movimiento de revolución alrededor del Sol y que la frecuencia del tono varía con la velocidad angular de los planetas medidas con respecto al Sol. Algunos planetas producen notas musicales constantes, por ejemplo la Tierra solo varía un semitono con una proporción de 16:15 o equivalentemente la diferencia entre una nota mi y un fa entre su afelio y su perihelio y Venus varía en un intervalo más reducido de 25:24. Kepler explica su razonamiento para deducir el reducido lapso de tonos propio de cada planeta en términos esotéricos.

La Tierra canta Mi, Fa, Mi: puede deducirse de estas sílabas que en nuestro hogar podemos esperar miseria y hambre (fa-mine).

En momentos muy poco frecuentes todos los planetas podrían tocar juntos en perfecta concordancia. Kepler propuso que esto podría haber ocurrido una única vez en la historia, quizás en el momento de la creación.

En un libro anterior Astronomía Nova, Kepler había escrito las dos primeras leyes del movimiento planetario. La tercera ley, que indica que el cubo de la distancia promedio del planeta al Sol es proporcional al cuadrado de su periodo orbital aparecía por primera vez en el capítulo 5 de este libro tras una larga discusión sobre astrología.

TEXTOS Ensayo en formato pdf KEPLER, Johannes: Harmonices Mundi (versión digital)

APLICACIÓN MULTIMEDIA Harmonice Mundi . Versión Multimedia (Aplicación Flash swf. 29 mb)

MOTETES (formato mp3 y pdf) Tristis est anima mea Ubi est Abel In me transierunt

Matemáticas y Geometría

Reproducimos un interesante ensayo sobre Matemáticas y Geometría en la más pura tradición Pitagórica.

En realidad son las Matemáticas y especialmente la Geometría, las bases pitagóricas sobre las que se apoya todo el Edificio Hermético. Así, tanto en Alquímia como en Astrología, ambas disciplinas están íntima e indisolublemente ligadas con ellas.

Mientras en Alquímia el peso y la medida, algo fundamental en esta disciplina hermética, están siempre asociadas, tanto a su praxis como a su desarrollo expresivo o iconográfíco, un vehículo usado desde siempre por los adeptos del Gran Arte para transmitir su conocimiento en forma velada. En Astrología también juegan un papel fundamental los denominados aspectos planetarios que son basicamente los preceptos de la Geometría Sagrada pitagórica aplicados al perpetuo desplazamiento de los cuerpos celestes en nuestro Sistema Solar. 

En definitiva, tanto en una como en otra cobra todo el sentido la frase de Platón: "En el Principio Dios Geometrizó".

Historia de los números irracionales

Pitágoras mantuvo una larga conversación con León, rey de Filo, y cuando éste le preguntó en qué consistía ser filósofo, qué hacía a un filósofo diferente de los demás hombres, el Maestro respondió:

“Estamos presentes en la vida como si se tratara de una gran feria. Cambiamos de ciudad, de una forma de vida a otra; algunos vienen para estar al servicio de la gloria, y otros del dinero, pero existen unos pocos elegidos que estudian el universo, y consideran que lo demás no es importante. Estos se llaman a sí mismo amantes de la sabiduría, en otras palabras, filósofos”.

El estudio de los números alogon y de la armonía, ha permitido al hombre comprender los mecanismos de la Creación, y establecer teoremas y leyes inherentes a los fenómenos terrestres.

A partir de estos números, y siempre aplicando los principios de la Geometría y a la Aritmética, planteamos una nueva concepción del universo conocido. Las líneas maestras seguidas se contraponen al pensamiento ortodoxo griego, pues se alejan del espacio euclidiano, y se adentran en la infinitud, tanto espacial como numérica, desterrando los tabúes que envuelven a la realidad de lo ilimitado.

Nuestros fundamentos se han basado en los cuatro Mathema: Aritmética, Geometría, Astronomía, Música, la tetrarkys pitagórica de la ciencia.

La figura representa la cuadratura del dodecaedro, que contiene los fundamentos geométricos y matemáticos utilizados en el diseño del Universo.

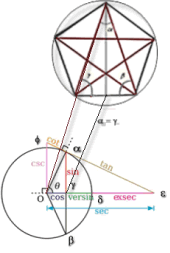
El emblema de la escuela pitagórica fue un pentágono regular estrellado. El pentalfa, así llamado, contenía la clave para formar el rectángulo de oro, determinado por la divina proporción, y tenido en cuenta por Fidias, al diseñar el templo de Atenea Parthenos.

La relación entre los lados de un pentáculo viene dada por la sección, (τομή), que refleja la relación entre el lado de un pentágono y su diagonal. Se trata del número áureo, un número de carácter sagrado que simboliza la armonía de todo lo creado:

1,618034…..

Platón, en el Timeo, lo describió como la clave del conocimiento físico del universo. Está presente en organismos vivos, en órbitas planetarias, en templos griegos y pirámides egipcias….

La simetría de este símbolo permite observar que dentro del pentágono interior es posible dibujar una nueva estrella, con una recurrencia ad infinitum.

Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. Lo que, llevado al plano cosmológico, equivale a asumir la existencia de mundos paralelos, en una sucesión infinita.

La unión de los vértices del pentágono forma una estrella compuesta por dos triángulos. El que está en posición derecha es un triángulo isósceles. Según los principios de la trigonometría, reflejados en el dibujo, el cociente entre cada lado y el seno de su ángulo opuesto es constante e igual al diámetro de la circunferencia circunscrita. A lados iguales se oponen ángulos iguales. a = g

Triángulos inscritos en circunferencias, como parte de las mismas. (Cuadrante)

El pentágono se encuentra aquí inscrito en una circunferencia, donde se refleja el segundo número sagrado, Pi.. Se trata de una constante matemática cuyo valor es igual a la proporción existente entre el perímetro de la circunferencia y la longitud de su diámetro. Una constante que aparecía ya en una lista numérica escrita para construir el gran templo de Salomón´

Pero fue una vez más en Grecia donde la exacta relación entre el diámetro y el perímetro de una circunferencia se convirtió en un desafío. Antiphon, inscribió en el círculo un cuadrado, luego un octógono e imaginó doblar el número de lados hasta el momento en que el polígono obtenido prácticamente coincidiera con el círculo.

Y Arquímedes desarrolló estos resultados. Demostró que la relación entre la longitud de la circunferencia y el diámetro era la misma que entre el área del círculo y el cuadrado del radio. Trazó un octógono regular inscrito en la circunferencia, y otro circunscrito a ella. Comprobó así que se podían construir sucesivamente polígonos inscritos y circunscritos a la circunferencia, duplicando cada vez el número de lados, lo que implicaba que sus áreas cada vez ser aproximaban más cercanas al área del círculo, que es .

De esta forma llegó a calcular las áreas de los polígonos de 96 lados, (96 = 2⁴ 6), obteniendo:

En la práctica, obtuvo un valor de 22/7 para ∏, y en la fase teórica, construyó la espiral que lleva su nombre, y que permitía rectificar la circunferencia y, por tanto, cuadrar el círculo.

Bastaba con el Teorema de Pitágoras para obtener una buena aproximación a ∏ :

Si partimos del perímetro conocido de un polígono regular de n lados inscrito en la circunferencia, entonces el perímetro del polígono regular de 2n lados se puede obtener aplicando 2 veces el Teorema.

Todas las operaciones aritméticas son posibles entre segmentos. Dados dos segmentos de longitudes a y b se pueden construir los segmentos de longitudes a + b, a – b, ab y a/b, así como la extracción de raíces cuadradas.

Si OQ = r, y siendo PQ = s el lado del polígono regular inscrito de n lados:

entonces OM =



 Luego MR = r- u, siendo RQ el lado del polígono de 2n = W

O tomando r = 1, l_n = S, l_2n = w queda l_2n =

  

Partiendo del hexágono, l₆ – 1:Para el dodecaedro.

3,14159…….La esencia la forma perfecta, el círculo, y los ciclos temporales, ∏

Pitágoras conoció en Egipto los sólidos regulares: tetraedro, hexaedro, octaedro e icosaedro. Cuatro sólidos que tienen sus caras iguales. Y a cada sólido se le asoció un elemento. (Agua, aire, tierra y fuego).

El descubrimiento de un quinto sólido, también recayó en los pitagóricos

.

El dodecaedro, figura sólida de doce caras pentagonales, permite generar la estrella de cinco puntas mediante la unión alternada de sus vértices. Este descubrimiento, como veremos, fue el que llevó a los pitagóricos a considerar la integración del universo. De la misma forma se han integrado en este símbolo las principales figuras geométricas, con sus principios aritméticos.

La existencia de los cinco sólidos la tradujo en un teorema, -una verdad matemática- . Pitágoras concebía el universo como un ser viviente, cuyas medidas estaban hechas a escala de las del sistema planetario, de la Tierra y del propio hombre. El quinto sólido o dodecaedro, simbolizaba el espíritu universal o éter.

Platón utilizó los cinco sólidos para explicar el origen y la estructura del universo. Al observar que todos los cuerpos tienen caras, y que éstas pueden ser divididas en triángulos, generó los poliedros desde un triángulo rectángulo. Cada uno de los sólidos platónicos correspondía a uno de sus elementos básicos, los cuales estaban compuestos por ínfimas partículas con estructura poliédrica.

Así, la tierra estaba asociada al cubo,el fuego al tetraedro, el aire al octaedro, el agua al icosaedro, y finalmente el Universo como un todo, estaba asociado con el dodecaedro.

Thales de Mileto, maestro de Pitágoras, midió la altura de las pirámides, a través de la sombra que producían cuando una vara clavada verticalmente en el suelo producía una sombra igual a su altura. Para esto, los rayos del Sol debían tener una inclinación de 45º. Los alogón se hallan encerrados en la Gran Pirámide, pues su superficie total se halla dividida según la sección, apareciendo de nuevo a y W . El lado de su triángulo de sección es el lado de un pentágono, y el de su triángulo de cara, la relación entre el pentágono, que es lado de su triángulo de sección, y el lado de su triángulo de cara es el lado de un hexágono, hallándose ambos inscritos en el mismo círculo.

En uno de los textos herméticos dice el dios Thot : ¿No sabes, Asclepios, que Egipto es una imagen del cielo?

Sucesiones ad infinitum

Dado que una sucesión numérica es una secuencia de números ordenados, nos consta que los pitagóricos se interesaron desde el primer momento en la construcción de series infinitas. Anaximandro había hecho derivar lo limitado de lo ilimitado. Afirmaba que que “lo ilimitado (apeiron) es el inicio de todo”.

Pitágoras combinó esta noción con la del límite, que da forma a lo ilimitado. El cosmos, limitado está rodeado por lo ilimitado (el aire), y el mundo lo inhala. Los objetos del cosmos limitado no son pura limitación si no que tienen mezcla de lo ilimitado.

De esta forma, un número irracional pudo ser entendido como el límite de una suma infinita de números racionales (por ejemplo, su expansión decimal).

El filósofo Zenón de Elea consideró el problema de sumar una serie infinita para lograr un resultado finito, pero lo descartó por considerarlo imposible: el resultado fueron las paradojas que llevan su nombre. Argumentaba que una bisección ilimitada de un segmento de recta daría como resultado un segmento de recta de longitud cero y la suma sucesiva de ceros es cero, por lo que ponía en duda la concepción pitagórica sobre los procesos infinitos.

Aristóteles propuso una resolución filosófica a la paradoja, pero el contenido matemático de esta no quedó resuelto hasta que lo retomaron Demócrito y después Arquímides. Asimismo afrontó de forma más osada problema del infinito, estableciendo en su obra Física, dos clases diferentes de infinito: el infinito potencial, como un proceso constante de crecimiento que no termina nunca; y el infinito actual, concebido como obra terminada.

El descubrimiento de los números inconmensurables vino a confirmar que no existe una medida común a todas las magnitudes. El cálculo de magnitudes irracionales precisaba establecer una relación entre razones y proporciones numéricas. Los matemáticos griegos concibieron el método de exhaución para encontrar la medida del círculo. Se basaba en la hipótesis de que la diferencia entre la superficie de un círculo y uno de sus polígonos inscritos puede ser tan pequeña como se quiera; dependiendo del número de lados que contenga ese polígono.

Leucipo, Demócrito y Antifon hicieron aportaciones al método griego de exhaución, griego al que Eudoxo dio una base científica alrededor de 370 a. C. El método se llama exhaustivo ya que expande las áreas medidas de manera que cubran más y más del área requerida.

El infinito geométrico

Fue a través del método exhaustivo de Arquímedes como se halló que número infinito de subdivisiones geométricas progresivas podían alcanzar un resultado trigonométrico finito. (Año 225 a.C). Su primer avance importante fue considerar el área de un segmento de parábola como una serie de segmentos infinitos: área igual a ⁴/₃ del área del triángulo con los mismos base y vértice y es igual a ²/₃ del área del paralelogramo circunscrito. Arquímides construyó una secuencia infinita de triángulos empezando con uno de área A y añadiendo continuamente más triángulos entre los existentes y la parábola para obtener áreas :

A, A + A/₄, A + A/₄ + A/₁₆, A + A/₄ + A/₁₆ + A/₆₄, …

El área del segmento de la parábola es, por lo tanto:

A(1 + ¹/₄ + ¹/₄² + ¹/₄³ + …) = (⁴/₃)A.

Éste es por tanto el primer ejemplo conocido de suma de una serie infinita.

Arquímides usó el método exhaustivo para encontrar la aproximación al área de un círculo. A través de la reductio ad absurdum, fue capaz de resolver problemas mediante aproximaciones con determinado grado de precisión, especificando los límites entre los cuales se encontraba la respuesta correcta. Esta técnica recibe el nombre de método de exhaución, y fue el sistema que utilizó para aproximar el valor del número π, lo que ya explicamos anteriormente.

Consideramos que dicho método, conlleva una aproximación cautelosa a la infinitud, por lo que no dudamos en refutar el postulado de Euclides que afirma: “El todo es mayor que cada una de las partes“. Nuestro propósito matemático se cumple si podemos alcanzar una magnitud tan pequeña como queramos, a través de por la división continuada de una magnitud dada. Para ello nos atenemos en primer lugar al axioma de Eudoxo Arquímides:

“De dos magnitudes desiguales, líneas, superficies o sólidos, la diferencia entre la mayor y la menor, añadida a sí misma un número suficiente de veces, puede sobrepasar cualquier magnitud dada”.

En su obra Sobre la Esfera y el Cilindro, Arquímedes postula que cualquier magnitud, sumada a sí misma suficiente número de veces, puede exceder cualquier otra magnitud dada, lo que corrobora nuestra oposición al postulado de Arquímides. Cabe destacar la forma en que su ciencia se opuso a los dogmas de su época, lo que convirtió al sabio de Siracusa en objeto de críticas por los matemáticos ortodoxos.

Representa pues, Arquímedes, un ejemplo de capacidad creativa e innovadora.

Prescindiendo de elementos desfasados de la tradición científica alejandrina, propuso y perfeccionó, con originalidad e ingenio, métodos para el desarrollo de la ciencia de su tiempo.

En la misma línea, definida por Arquímides, trataremos de abordar problemas geométricos utilizando los números.

Una de las clasificaciones de los números realizadas por los pitagóricos, era según sus formas poligonales. Para ello, los representaban sobre la arena con pequeñas piedras redondas, según las diferentes formas geométricas que adoptaban (triangulares, cuadrados, pentagonales…) Se crearon así las primeras sucesiones de números, a los que denominaron números poligonales o figurados.

A partir de estos números poligonales, y siguiendo la metodología pitagórica, , nos hemos apoyado en los dibujos para realizar nuestros cálculos.

A través de la suma de la unidad, se obtiene el dos, representado por los dos puntos extremos de una recta, y si se siguen añadiendo unidades, pueden obtenerse todos los números representados por dos, tres, cuatro… como puntos alineados. Se obtiene de esta manera el desarrollo lineal de los números.

Por tanto podemos afirmar que las sucesiones de estos primeros números cuadrangulares, constituyen la primera versión del las sucesiones numéricas infinitas, considerando la relación entre órdenes consecutivos de números de un determinado tipo y relaciones entre números poligonales de tipos diferentes. Así, por ejemplo, si llamamos T(n), C(n), P(n), H(n) al n-ésimo número triangular, cuadrado, pentagonal y hexagonal, respectivamente, obtenemos importantes propiedades aritméticas de los números enteros, que, a su vez podemos visualizar en las siguientes figuras:

Si partiendo de la unidad vamos añadiendo sucesivamente los números impares conforme al “gnomon”, obtenemos los números cuadrados, mientras que si partimos de dos y le vamos añadiendo los números pares, obtenemos los números triangulares.

n(n + 1)/2

Aritméticamente basta escribir en una primera fila los números impares y proceder para la segunda como en los números triangulares, para obtener los números cuadrados:

1 3 5 7 9 11 13 15 17

(Cada número es el anterior + 2)

1 4 9 16 25 36 49 64 81

(Cada número es el cuadrado de la serie de números naturales).

De aquí esta importante propiedad: La suma de los n primeros números impares es igual al n^enésimo número cuadrado. Un cuadrado es un número en forma de rectángulo cuyos lados contienen un número igual de puntos.

Un número de forma rectangular era llamado heterómeco si un lado contenía un solo punto de más que el otro lado, y era llamado promeco si la diferencia entre los puntos de ambos lados era mayor que uno. Por ejemplo el número 15 es promeco y el número 20 heterómeco.

Llevando sobre un lado y paralelamente a una diagonal una línea recta, ésta divide a un número heterómeco en dos partes que son dos triángulos rectángulos iguales:







Y como el número de puntos del n^enésimo heterómeco, constituido por n columnas y por n + 1 filas, es n (n + 1), resulta para el n^enésimo número triangular la fórmula n (n + 1). Recordando la definición del número triangular, se tiene:



Observando la figura podemos deducir que todo numero cuadrado (de cualquier orden) es la suma de un número triangular del mismo orden y otro de orden inmediatamente anterior. Por ejemplo: 9 = 6 + 3, 25 = 15 + 10. Esto se puede representar de esta forma: C(n) = T(n) + T(n – 1).

Un número pentagonal se puede obtener como la suma de uno triangular del mismo orden más dos veces otro de orden inmediatamente anterior. Por ejemplo: 22 = 10 + 2.6. Eso se puede representar de esta forma: P(n) = T(n) + 2T(n – 1).

El número pentagonal n—ésimo es igual a n más tres veces el número triangular(n—1). El proceso puede continuar indefinidamente, es decir, ad infinitum, con lo que empezamos a aplicar el infinito potencial.

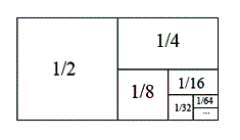
Nos consta que los egipcios sabían cómo sumar una serie geométrica. Como ejemplo, suponemos un rectángulo de área 1:

Si lo dividimos en rectángulos más pequeños, podemos calcular el área de cada uno :



Si colocamos cada sumando en filas, la suma de éstas se puede calcular hallando la suma de cada columna:



Del mismo modo que con la serie geométrica, calculamos ahora los inversos de los números triangulares (1, 3, 6, 10, 15….)



Pero calculamos no la suma, sino su mitad:

1/2 · S = 1/2 + 1/6 + 1/12 + 1/20 + … =

=(1- 1/2)+(1/2 – 1/3)+(1/3 – 1/4)+(1/4 – 1/5)… =

= 1- 1/2+1/2 – 1/3+1/3 – 1/4+1/4 – 1/5… = 1

Luego S = 2

Tenemos una aproximación al valor buscado: 2,71.

Sustituimos términos, obteniendo la siguiente fórmula:

Se trata de una sucesión creciente y acotada, y por tanto, convergente. Su límite es un número irracional (alogón), al que hemos llamado épsilon, (e).

Según Arquímides:

“Hay algunos que creen que el número de granos de arena es infinito en cantidad y por arena…. Hay también algunos que, sin considerarlo infinito, creen que no existe una cifra lo bastante grande para exceder a su magnitud. Intentaré demostraros por medio de puntos geométricos que los números nombrados por mí…. algunos exceden no sólo al número de la masa de arena igual en magnitud a la de la Tierra, sino al de la masa igual en magnitud al Universo”.

                                                                                                                          Arenario. Arquímides.

Hemos reproducido este fragmento de la obra de Arquímides, para señalar cómo éste, una vez más, no tuvo reparos en traspasar los límites matemáticos tradicionales, abordando un sistema de numeración basado en números espectacularmente grandes. Partiendo de una miríada o 10.000 como unidad de primer orden, obtenía por extensión el número (10.000)2, llegando hasta (100.000)2, como unidad de tercer orden, y extendido llegaría a (100.000)3. Podríamos continuar hasta llegar al término n-ésimo, al que llamaremos N (100.000.000)100.000.000 o N elevado a 108, para el primer octeto.

La idea de Apolonio para extender el sistema de numeración a números más largos, capaces de superar el número de partículas del universo, fue trabajar con potencias de la miríada. Así, una M con una a sobre ella representaba (10000), M con b sobre ella representaba M² (10000000), y así sucesivamente. Era un sistema similar al usado por Arquímides, pero en el de Apolonio, la base a la que eran elevadas las diversas potencias era 10000 = 10⁴ .

Aplicamos nuestra fórmula anterior a este sistema, para una primera potencia (12), pues estos son los meses del año, lo que está en relación con nuestro cálculo final.

Aplicando fórmula del límite de sucesiones infinitas que hemos obtenido:



Comprobamos que:

= 2,61303…, valor que nos permite obtener dos aproximaciones:

¨ Al número alogón al cuadrado: a ² = 1,6180339887499)² = 2,618….)

¨ Al número que buscamos, 2,71, en e una segunda aproximación.

Sustituimos por la base de Apolonio:

Con lo cual, obtenemos exactamente nuestro número. Podemos ya definirlo como el límite de (1 + ¹/_n)ⁿ cuando n tiende a infinito. Es el límite de la sucesión de término general.

Junto a la demostración geométrica del teorema de Pitágoras fue encontrado el método para hallar la serie ilimitada de las ternas de números “pitagóricos”, esto es, ternas de números que satisfacen la ecuación a²+b²=c². y que tienen la forma:

n, (n² – 1)/2, (n² + 1)/2, donde n es impar.

Otra regla sería: n, (n/2)² – 1, (n/2)² + 1, donde n es par, y se cita en las obras de Platón.

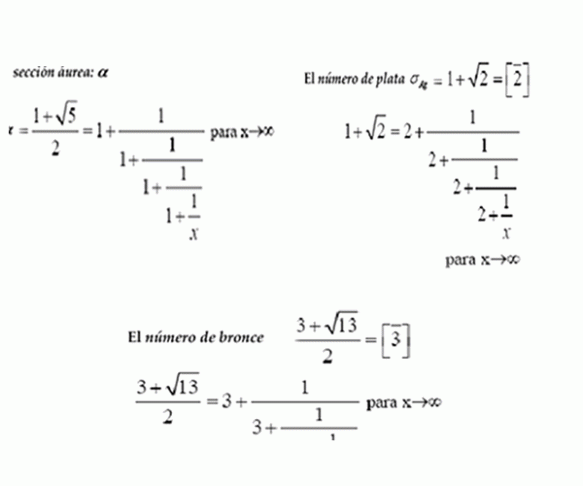
Por último, el número e se puede representar como una fracción simple continua infinita,al igual los alogós phi y ∏, y los números metálicos:

Desarrollo en fracciones continuas de los números metálicos:

Paisaje curvo

La Geometría surge en la prácticas primitivas de la agrimensura egipcia. De hecho, hecho, Geometría significa “medir la Tierra”. Esta antigua geometría empírica pronto fue transformada por los griegos en matemática.

Tales de Mileto, dos siglos (A.UC), puede considerarse el fundador de esta nueva geometría sistemática, asociada a métodos deductivos, y al razonamiento lógico.

El continuador fue Pitágoras de Samos.

Los sabios han indagado en las misteriosas formas curvas, presentes en la Naturaleza y el Universo, desde la humilde concha de un caracol o la tela de una araña, hasta las formas estelares. Aunque solemos decir que Arquímides es el pionero en describir curvas mecánicas, basadas en el movimiento de un punto, fue precedido por compatriotas suyos: Hipias de Elis, y Dinóstrato, llamado el padre de las cónicas, quienes inventaron una curiosa curva generada por el movimiento uniforme de dos rectas, a la que llamaron cuadratiz de Dinóstrato, y que también aplicaron para trisecar el ángulo.

Menecmo presenta estas curvas como secciones de un cono circular recto por un plano perpendicular a una generatriz, por lo que la parábola fue llamada sección de cono rectángulo. La elipse era la sección de cono acutánulo, y la hipérbola, la sección de cono obtusángulo.

Apolonio de Perga fue contemporáneo de Arquímedes (286 a. de J.C. – 212 a. de J.C.), Vivió la mayor parte de su vida en Alejandría y se le recuerda como “el gran geómetra”.

Perfeccionó las matemáticas helénicas, especialmente la Geometría. Su obra fundamental fueron ocho libros sobre las secciones cónicas, donde demuestra que tanto la circunferencia como la elipse, la parábola o la hipérbola pueden determinarse al cortar un cono con planos de distinta inclinación (por lo que estas curvas son llamadas Cónica. En el libro V se introducen nociones tales como normal a una curva, evoluta, centro de curvatura, etc. El estudio de las curvas de segundo grado fue llevado a la cúspide de la perfección.

A finales del siglo IV (AUC), existían ya dos obras importantes sobre cónicas: el Libro de los lugares sólidos, de Aristeo, y una obra de Euclides, en cuatro libros, en la que se continúa con lo expuesto en las Cónicas de Apolonio.

Y aun antes de Arquímides, los matemáticos de épocas antiguas habían comprobado que las superficies curvas contienen un elemento de irracionalidad que dificulta su medida. Tal y como su caprichosa forma sugiere, se trata de curvas fugaces, en aparente movimiento. No son curvas estáticas, como las cónicas o las lúnulas, y su trazado debe ser, pues, mecánico y complejo. Podríamos definirlas de la siguiente forma:

“Son curvas planas que comienzan en un punto y cuya curvatura va disminuyendo progresivamente a medida que aumenta su radio de curvatura.”

Arquímedes de Siracusa, admirado ante la belleza de esta curva, realizó un estudio profundo sobre sus propiedades, en un escrito titulado “De las espirales” desde entonces se la conoce como espiral de Arquimedes.La forma en se produzca ese cambio de curvatura y ese incremento del radio de curvatura nos colocará ante diferentes tipos de espirales. La distancia al origen y el ángulo girado hasta llegar a ese punto son los dos parámetros que definen una espiral.

En una espiral de Arquímedes las distancias entre sus brazos, a y b son constantes.

Ahora veremos la primera forma en que hemos deducido el tercer número alogón, e. Para ello hemos centrado nuestra atención en las curvas presentes en nuestro entorno, identificando otro tipo de espiral en diversas formas de la Naturaleza, como la concha del caracol., a la que llamaremos spira crescendis.

La espiral creciente (spira crescendis),o geométrica, se distingue de la espiral de Arquímides por el hecho de que las distancias entre su brazos se incrementan en progresión geométrica, mientras que en una espiral de Arquímedes estas distancias, a y b son constantes.

(De igual forma, la espiral creciente, puede ser generada a partir de rectángulos comprendidos en la sección,. Podemos, por tanto, relacionar a e con phi y ∏ a partir de dicha espiral).

Es decir, el radio de posición en un punto no depende de forma lineal, sino creciente y uniforme del ángulo girado. Según vayamos girando alrededor del origen la curva se va ir alejando del origen de forma cada vez más rápida.

La espiral ascendente está generada por el número e en una fórmula abierta, = a e ^bq,donde a y b son distancias constantes, e es nuestro número alogón e = 2, 71828182, r el radio de posición de un punto y theta el ángulo girado. Esta espiral crece hacia el infinito en progresión geométrica.

Teodoro de Cirene (siglo IV a. C), fue maestro de Platón, y, según éste, el primero en demostrar que las raíces cuadradas de los números naturales (no cuadrados) desde el 3 al 17, son números irracionales. Utilizando el teorema de Pitágoras, representó las raíces de los números naturales; añadió perpendicularmente a un segmento una unidad lo que forma triángulos cuyas hipotenusas son las sucesivas raíces, y dando forma a una espiral conocida como Espiral pitagórica, que coincide con nuestra espiral creciente.

Uno de los catetos de cada uno de los triángulos rectángulos consecutivos que forman la espiral, mide la unidad, el otro es raíz cuadrada de n y la hipotenusa es raíz cuadrada de n + 1.

Pitágoras insistía en que esta espiral era la figura que mejor representaba la existencia, teniendo en cuenta la evolución, ya que los sucesos no se repiten con exactitud, sino que se retorna a una posición parecida, pero algo alejada de la anterior. Simboliza desarrollo, continuidad cíclica pero en progreso, y rotación creadora. También nacimiento y muerte, o más bien muerte iniciática y el renacimiento a una nueva existencia en un plano superior.

La espiral ascendente es la única curva que verifica que su evoluta, su involuta, su cáustica y su podaria son, a su vez, una espiral ascendente. Por ello “eadem mutata resurgo” significa que aunque me cambien, es decir si trazan mi evoluta, mi involuta, mi cáustica de reflexión o de refracción… siempre volveré a aparecer semejante a mí misma.

Este tipo de espiral parece también en la genealogía de ciertas especies. Es el caso de los machos o zánganos de una colmena. La clave está en que las abejas hembras de la colmena nacen de los huevos fertilizados (tienen padre y madre), mientras los machos o zánganos nacen a partir de huevos no fertilizados, o lo que es lo mismo, sólo tienen madre. De esta forma, sus árboles genealógicos siguen estrictamente una distribución de Fibonacci: un macho (1) no tiene padre, sino una madre (1,1), dos abuelos – padres de la reina – (1,1,2), tres bisabuelos – porque el padre de la reina sólo tiene madre – (1,1,2,3), cinco tatarabuelos (1,1,2,3,5), etc.

La espiral pitagórica viene definida por unos números, a los que llamaremos λόγος (logos donde una serie aritmética de logos corresponde a una serie geométrica de números. Estas sucesiones eran ya conocidas por Pitágoras, quien las reconoció como progresiones geométricas, la primera en relación 2 : 1, y la segunda, en relación 3 : 1.

El nombre que les dio fue el se la Doble Tetraktys.

1	2	4	8
1	3	9	27



Platón utilizó esta Tetraktys para formar el alma cósmica, añadiéndola al círculo para representar los siete planetas, y las distancias entre ellos. Esto nos permite afirmar que la espiral definida por estas progresiones, la espiral creciente se encuentra en nuestro Universo, siendo una de las formas que adoptan los cuerpos estelares.

La Doble Tetraktys fue símbolo de las progresiones: el punto, (1), que se transforma en línea (3 y 2), formando el plano (4 y 9), hasta llegar al sólido o cubo (8 = 2³, 27 = 3³). 

El resultado final es el origen de los sólidos ya descritos. Completa el constante proceso de cambio que transforma a las formas físicas: (Puntos, líneas, alfas, superficies y sólidos de tres dimensiones).

El universo de Pitágoras

La filosofía de Pitágoras, (ca.582 –500 a.C), el gran filósofo y matemático griego, se conoce sólo a través de la obra de sus discípulos. Fueron sucesores de los órficos, y como ellos creyeron en la inmortalidad y la transmigración del alma.

Al igual que lo había sido Orfeo, Pitágoras fue un virtuoso músico y tañedor de lira, instaurando la educación musical en Grecia, la cual entendía como vehículo de unión entre el hombre y el cosmos.

Pitágoras fue el instaurador de la educación musical en Grecia, entendiendo la música como una ciencia numérica que significaba la unión entre el hombre y el cosmos. Se manifestaba capaz de escuchar la música emitida por los cuerpos celestes, la cual imitaba con su lira, para encaminar el alma hacia su liberación final.

Revolucionó la música, la astronomía, la religión y las matemáticas, descubriendo los fundamentos matemáticos de las consonancias musicales de forma casual y sensorial, a través de los golpes de un herrero. Su filosofía integró doctrinas de espiritualidad afín de la India y Egipto, sobre las que proyectó la luz de la racionalidad y la libertad helénicas.

Fue instruido e iniciado en las matemáticas sagradas y las ciencias de los principios universales por los sacerdotes de Memphis en Egipto, superando las más duras pruebas en una iniciación que duró veintidós años, y que estuvo a cargo del sumo sacerdote Sonchis.Pitágoras atribuyó cualidades universales a los símbolos geométricos y estableció sus correspondencias numéricas.

La unión de las tres formas geométricas clave configuró elementos tales como :

• El Círculo (símbolo de la Eternidad),
• El triángulo (para la creación), y
• La Ley de Siete o de la Octava (para el funcionamiento de lo creado).

El círculo

Es una forma geométrica perfecta que representa lo Absoluto, sin principio ni fin. Se concibe como la unidad y también como la totalidad.

Las diferentes culturas han usado símbolos que lo representan: el ouroboros o “dragón alquímico”, o la serpiente que se muerde la cola en Egipto , como imagen de la naturaleza cíclica y eterna del universo. Este significado fue usado posteriormente por gnósticos, cabalistas y alquimistas. Está asociado al 1: el absoluto o unidad no polarizada.

El triángulo

El triángulo equilátero simboliza la inteligencia superior y los tres atributos divinos: fuerza, belleza y sabiduría, en correspondencia con las tres potencias creadoras: acción positiva o impulsora, negativa o receptora y neutra o conciliadora. Intelecto, sentimiento y voluntad en el plano humano.

La clave numérica sería el 3: entendido como el principio de reconciliación de contrarios, la Trinidad cristiana y omnipresente en casi todas las mitologías.

Cuadrado

“En la geometría plana, el círculo es símbolo del cielo y el cuadrado de la tierra, y el octógono intermedia entre uno y otro, y a través de él se logra la cuadratura del círculo, la unión indisoluble del espíritu y la materia”. El cuadrado inscrito en el círculo representa la materia potencial contenida en la unidad.

La gran octava cósmica

Si se considera una cuerda de una longitud igual a la unidad y se hace vibrar, emitirá un sonido. Si se la sujeta por la mitad y se hace vibrar de nuevo, emitirá un sonido una octava más alto. Entre la nota original y su octava habrá siete intervalos, etapas desiguales que el oído interpreta como sonidos armónicos, proporcionando sensación de equilibrio, de orden. Es una forma de explicar la escisión del 1 en la multiplicidad, el 2.

El 7 significa la unión del espíritu (el 3) y la materia (el 4), expresada por la forma geométrica de la pirámide: estructura de base cuadrada que simboliza los cuatro elementos, y lados triangulares, las tres modalidades del espíritu.

Tanto el 3 como el 7 son “números de movimiento perpetuo”:

3: El número de la relación, de la trinidad mística tres-en-uno.

7: El número del crecimiento, del progreso, de la armonía, del movimiento perpetuo, que da la misma secuencia repetitiva cuando se divide la unidad.

1/3 = 0,3333333…
1/7 = 0,1428571428571…

El Pentagrama:

El pentáculo o pentalfa es un antiguo símbolo pagano, formado por un triángulo equilátero encerrado en círculo, y éste a su vez inscrito en un cuadrado. Esta estrella pentagonal se convirtió en el símbolo de los discípulos de Pitágoras. Según su filosofía, la realidad y el universo estaban constituido según un orden numérico formado sólo por números fraccionarios, en una proporción que expresaba las verdades esenciales de la existencia.

En el pentáculo, el número áureo sería la relación entre el lado del pentágono regular y la recta que une dos vértices no consecutivos de éste. Si se toma como unidad un lado del pentágono interior, cualquier línea que marca los brazos de la estrella mide f. Al medir la longitud total de una de las cinco líneas del pentágono interior resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea f. También la longitud total de cualquiera de las cinco líneas que atraviesan la estrella mide Φ3, mientras que la suma del lado interior y cualquiera de sus brazos es Φ2.

Por su gran simetría, dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito.

El pentagrama fue acogido por la iglesia católica para representar a la Virgen María, y también por Leonardo da Vinci para inscribir en él al hombre de Vitruvio, en orden a demostrar el principio de que “el hombre es la medida de todas las cosas.”

El Eneagrama

El Eneagrama (del griego εννεα, ennea, “nueve”, y γράμμα, gramma, “trazo”) es un símbolo universal geométrico compuesto por nueve elementos (números) ubicados dentro de un círculo, dentro del cual se encuentran circunscritos un hexagrama y un triángulo equilátero. Representa así la acción creadora del 7 que atraviesa al 3 (la triple naturaleza de la unidad).

Sus orígenes se remontan a más de dos milenios atrás en el tiempo; no obstante, su utilización como sistema iniciático entronca con las tradiciones de transmisión oral entre maestro y discípulo. Fue en la primera mitad del siglo XX que George Gurdjieff (1877-1949) lo introdujo en Europa y lo utilizó en su escuela del Cuarto Camino, tras haber recibido sus “secretos” de la orden sufí naqsbandi. Generalmente, se le atribuyen los primeros esfuerzos en difundir el Eneagrama en occidente a G. I. Gurdjieff. Tras él vinieron otros tratadistas y estudiosos de importancia, tales como Oscar Ichazo, Claudio Naranjo y más modernamente Helen Palmer, Don Richard Risso y otros.

El uso del Eneagrama incluye, entre muchas otras interpretaciones, el estudio de la personalidad desde 9 tipologías. Los nueve puntos de contacto de las figuras con el círculo, en psicología se refieren a los nueve tipos fundamentales de personalidad o eneatipos . Pero ésta es una faceta a la cual no vamos a referirnos aquí.

El Eneagrama explica cómo funciona algo y cómo evoluciona y se desarrolla ese proceso en particular. Los otros símbolos acompañantes, son “morfológicos”, y muestran cómo es la estructura de las cosas contenidas en este Universo. Esto sí que nos atañe.

Hexagrama

El hexagrama, en conjunción con el círculo, se refiere a la ley del 7 o ley de la octava. Si dividimos 1 entre 7, encontramos el 0 como unidad, y una serie de seis dígitos decimales: 0,142857… Asimismo, si consideramos que la unidad viene representada por el círculo y dividimos los 360 grados que tiene el círculo entre 7, volvemos a encontrar los mismos dígitos como decimales: 51,428571… La suma de las seis cifras que se repiten periódicamente (1+4+2+8+5+7) da 9.

Los números sagrados

Pitágoras aportó como idea original el uso simbólico y alegórico de los números, por los que sustituyó a los dioses, sentando las bases de la filosofía platónica.

1 : Poderoso símbolo metafísico que no se consideraba un número en sí, sino el creador de números, junto con el dos, (la diada).

El uno absoluto, asemejado al Caos, que ponía el marcha el proceso cósmico, como origen de lo finito, y de los números impares.

2 : La polarización. Origen de lo infinito, lo irracional.

3 : Considerado como el primer número verdadero, origen de la pluralidad. Se le atribuían propiedades místicas y mágicas, en las tríadas paganas y la Trinidad cristiana. Origen de interminables disputas entre las teologías, que trataban de materializar de forma razonada un concepto puramente abstracto. Representa el principio de armonización de contrarios, (el 1 y el 2), señalando las tres partes del cosmos:

Principio — Punto medio — Final. 1 2 3= La forma completa.

Según Platón, en su Timeo: “No es posible unir bien dos elementos aislados sin un tercero, ya que es necesario un vínculo en el medio que los una.”

Según los neoplatónicos, el principio de todo lo existente es la unidad absoluta, lo Uno, realidad suprema, de la que surgen todas las demás realidades por emanación. El primer ser emanado del Uno es el Logos, llamado también Verbo, Inteligencia, que contiene las ideas de las cosas posibles. Después, la Inteligencia engendra el Alma, principio del movimiento y de la materia. El Uno, la Inteligencia y el Alma son las tres hipóstasis de la Trinidad neoplatónica Para que el Alma se una al primer principio es preciso que supere el pensamiento y que, por el éxtasis, se confunda con Dios y pierda toda consciencia de sí misma.

El significado mágico del número 3 está igualmente representado en la naturaleza triple de la Hécate lunar. Y son tres las veces que los magos, normalmente repiten sus invocaciones:

“La sacerdotisa, tres veces, con una voz de trueno, invocó a los cien dioses, el Erebo, el Caos, la triple Hécate, los tres rostros de la virgen Diana. “

La alquimia no difiere en sus consideraciones, indicando que la creación se produjo mediante la interacción de tres principios: el azufre, el mercurio y la sal.Así, pues, formuló que las tres leyes universales fundamentales que regulan toda manifestación son:

1. La ley de la unidad : todo surge y tiende a la unidad , porque lo creado lleva un su interior la semilla de su creador.

2. La ley de la correspondencia : como arriba, así es abajo . El universo y, por consiguiente, el ser humano, es un holograma. La parte contiene el todo.

3. La ley de semejanza : lo semejante se atrae . Es un principio electromagnético que no se refiere a la polaridad, sino a la vibración.

5 : 2 (polaridad) + 3 (reconciliación entre contrarios). Representa la unión de los principios masculino y femenino. Número de la potencialidad. Gobernó las proporciones de las catedrales góticas.

Simbolizaba las formas poligonales:

• Pirámide Fuego
• Cubo Tierra
• Octaedro Aire
• Icosaedro Agua
• Dodecaedro: Éter

Sección áurea: donde la escisión primordial rige el flujo de los números hasta el cinco.

6 : Número del mundo, el tiempo y el espacio. Rige los fenómenos espaciales y temporales. Representado por el Sello de Salomón.

7: Representa el crecimiento, las etapas en las que se completan los fenómenos.

3 + 4 = 7: unión del espíritu y la materia, lo que viene expresado por la estructura piramidal:

De acuerdo con el sistema de cultura oculta oriental existen 49 centros nerviosos sagrados en el cuerpo humano, de los cuales los siete más importantes y centros clave están situados cerca de la espina dorsal a diversos intervalos.

El número total, 49, es el cuadrado de 7, y es también el número de rondas y subrondas de una cadena planetaria.

8: El mundo físico: (6 veces 2).

9: Número que posee tres veces el tres, número perfecto por excelencia. La gran Enéada

El tetraktys

Es el símbolo de mayor contenido sagrado entre los pitagóricos. Expresa el mundo ideal de Platón.

Contiene las claves de la armonía, que rigen la creación según una relación proporcional:

1 + 2 + 3 + 4 = 10

3/ 4 = la cuarta (diatessaron)
2/3 = la quinta (diapente)
1/2 = la octava (diapasón)
4/ 1 = la doble octava.

Las Musas

Llámese musa a la fuente de inspiración destinada a consumar el impulso creativo. El hecho preeminente es que conduce a una relación con planos superiores —entiéndanse como divinos—, por encima de las limitaciones de la dinámica puramente mental. El origen de esta figura es impreciso, pero Homero ya les otorgaba el número nueve: “Nueve Musas cantando por turno con voz melodiosa entonaron sus trenos” Los pitagóricos, ya hemos visto, asociaron el número nueve con la perfección, y seguiremos observando cómo crearon verdadero culto a estas Musas.

El Parnaso ilustra de forma pictórica la alegoría de Apolo y las Nueve Musas.

Al igual que la música, las composiciones pictóricas debían ser elaboradas de acuerdo a una clave. Al De este modo, los pintores del Renacimiento utilizaron una progresión geométrica (4, 6, 9), 4/6 = 6/9 = 2/3, a la que se adapta el cuadro de Poussin. Platón ya advirtió sobre la necesidad de contar con al menos tres puntos para establecer una óptima proporción, con lo que de nuevo nos hallamos frente al número mágico, el tres.

Poussin estaba familiarizado con la teoría musical de la época, que conocía perfectamente.

Las escuelas pitagóricas se configuraban a modo de templos dedicados a las Musas. Pretendían integrarse como un universo, centros de culto al conocimiento, transformadores de conciencias a través del ejercicio de las artes, el estudio y la lectura de textos sagrados.

El significado del término museo era el de altar dedicado a las musas, y músicos, la palabra que designaba la condición de estar bien versado en cuestiones de la mente, pues según Platón la música guarda estrecha relación con todos los procesos mentales.

Perseverando en la tarea de recabar puntos de contacto entre las diferentes doctrinas, encontramos que la instrucción egipcia, como la pitagórica, se integraba como un todo: el hombre era tenido como imagen de la creación. Las medidas humanas estaban hechas a escala de las medidas universales, en una proporción Tierra — Hombre— Cosmos, entendidos como partes de la Totalidad.

Las escuelas pitagóricas se configuraban a modo de templos dedicados a las Musas. Pretendían integrarse como un universo, centros de culto al conocimiento, transformadores de conciencias a través del ejercicio de las artes, el estudio y la lectura de textos sagrados.

El significado del término museo era el de altar dedicado a las musas, y músicos, la palabra que designaba la condición de estar bien versado en cuestiones de la mente, pues según Platón la música guarda estrecha relación con todos los procesos mentales.

Perseverando en la tarea de recabar puntos de contacto entre las diferentes doctrinas, encontramos que la instrucción egipcia, como la pitagórica, se integraba como un todo: el hombre era tenido como imagen de la creación. Las medidas humanas estaban hechas a escala de las medidas universales, en una proporción Tierra — Hombre— Cosmos, entendidos como partes de la Totalidad.

 

La armonía de las esferas

Mentis Apollinae vis has movet, undique musas.

Pitágoras fue el primero en utilizar el término Cosmos para describir el orden y la armonía inherentes a un universo regido por unas leyes cognoscibles e inteligibles por el hombre a través del número que es el principio elemental, «la esencia de todas las cosas», componente esencial de la armonía matemática que debe guiar, con finalidad religiosa, toda investigación sobre el universo. Pitágoras alcanzaría esta iluminación, tras sus viajes, a través de su propia reflexión sobre la sabiduría milenaria de los pueblos de Oriente Próximo. De los egipcios aprendería que las formas de las figuras geométricas se ajustan a números y proporciones y de Mesopotamia que los movimientos de los astros están regidos por leyes numéricas. De su propia experimentación, Pitágoras deduce que la armonía musical también está regida por el número. De estos tres hechos, tras una audaz extrapolación, Pitágoras estableció que «el número es la esencia del universo» y que «el número es la raíz y fuente de la naturaleza eterna».

Renacimiento

Ya hemos visto cómo a lo largo de todas las épocas se ha tratado de representar el cosmos de muy diversos modos, y siempre en forma de alegorías, difíciles de interpretar para los profanos.

El arte del Renacimiento ofrece múltiples evidencias. Botticelli y Policiano representaron el Nacimiento de Venus sin velos: tanto en el poema de Policiano, como en el cuadro de Botticelli, la blanca espuma de las olas simboliza el esperma divino caído del cielo. La alegoría encierra un mito cosmogónico y muestra cómo el espíritu divino, en palabras de Plutarco, “es transformado y diseminado en vientos y aguas”, se representa el instante que sigue al nacimiento cósmico: la Venus recién nacida, surgida ya del mar, es empujada a tierra firme por los vientos de la primavera.

Y sin duda una de las creaciones alegóricas más representativa por su innegable analogía con el relato de Dante, corresponde a la obra neoplatónica, titulada “La música de las esferas”, probablemente realizada por Leonardo Da Vinci para servir de portada al tratado sobre música escrito por Franchinus Gafurius De Practica Musice, publicado en Milán en 1496.

Pitágoras una vez más había utilizado la escala armónica musical para mostrar el funcionamiento y ordenación del cosmos, y el diagrama de Gafurius reproduce su concepción, de forma simbólica En él, el Universo entero se nos presenta encerrado dentro de nueve círculos o esferas, cuyos perfectos movimientos producen una armonía, que crea una música divina, inaudible, la cual se expande por todo el Universo. Pero éste no es el único ejemplo que plasma su filosofía. En el Sueño de Escipión, la obra más representativa del género neoplatónico, Cicerón narra cómo el universo se halla estructurado dentro de nueve círculos o esferas que se mueven en completa armonía. Dicha armonía está formada por intervalos desiguales que guardan una perfecta proporción, y el oído interpreta como armónicos, creando una música divina, inaudible, que se expande como el resto del Universo, constituyendo su voz.

En la Música de las Esferas de Gafurius, las tríadas de las Gracias y de Serapis se colocan en los extremos opuestos de la gran escala cósmica, representando el mundo ctónico. El Universo entero, desde lo más alto hasta lo más bajo, aparece supeditado al ritmo triádico marcado por el propio Apolo. Lo que pretende expresar que el Tiempo surge de la Eternidad, que la progresión de la serpiente depende de la relación con la esfera más alta, donde su cola se enrosca en un círculo, sobre el que se levanta Apolo. El espíritu, en su envoltura carnal, debe enfrentarse al tiempo, (el oscuro valle), sus trampas terrenales que le confunden y alejan del orden universal, en un camino lleno de vicisitudes, como el narrado por Dante o Apuleyo.

Pero las Musas, a través de la inspiración de las Artes divinizadas, le guiarán de nuevo hasta la cima, “y vi que su cima ya vestía los rayos del planeta que lleva recto por cualquier camino”,  donde reside la Luz absoluta de Apolo.

En lo alto, las Tres Gracias aparecen a la derecha de Apolo, que con su lira de siete cuerdas (heptacorde), simboliza las consonancias musicales y planetarias, dirige la danza, al tiempo que anima a las esferas celestes, que se despliegan a sus pies, con sus sones. Gafurius lo expresó diciendo: “Las Musas, los planetas, los Modos y las cuerdas se corresponden unos con otros.”

Las esferas se emparejan en consonancia con las Musas, a excepción de Thalía que se asocia al planeta Tierra. Al final de la escala, la trinidad de Serapis se cierne sobre las últimas y más bajas de las emanaciones musicales, las tres cabezas animales, que simbolizan el tiempo devorador en sus tres aspectos —pasado(lobo), presente, (león), y futuro (perro), identificado con Cerbero, guardián del reino subterráneo.

Todo ello ha sido representado del siguiente modo:

La interpretación sería la siguiente: Se trata de un sistema de 7 planetas, cuyos sus movimientos emiten notas que se corresponden con las notas del heptacorde.

Las Musas en número de 9, están divididas en 3 tríadas simétricas, ( 3 . 3), y su raíz cuadrada, el 3, representa la Trinidad, encarnada por las tres Gracias que aparecen junto a Apolo. (Ya se ha hablado del simbolismo del 3 y el 9). Se sitúan en proporción a las claves enunciadas en el tetrarkys, creándose los intervalos musicales de 1 tono, según la relación armónica o subcontraria.

La nota asociada a Apolo, el Sol, se sitúa en el centro, pero en realidad habría tres notas por debajo de ella y cuatro notas por encima; la última de éstas sería la nota más alta de la octava, que pertenece a la musa Urania. Esta nota trasciende completamente la música planetaria y se halla en la esfera de las estrellas fijas.

La división de la octava resultante, con la cuarta nota tratada como central y la octava como trascendente mientras las seis restantes forman tríadas simétricas, corresponde de manera fiel a la composición de la Primavera. transportada a la clave de Apolo

La escala musical pitagórica inicial podía ampliar su alcance añadiendo cuerdas. La 8ª cuerda fue añadida por Licaón de Samos, por lo que Platón basó su música cósmica en la lira de ocho cuerdas, u octacorde. (Versión de la República).

Este universo musical también aparecía en La Divina Comedia de Dante, en el Paraíso, en cuyo Primer Canto, y antes de recorrer las nueve esferas móviles, donde están situadas las almas de los santos, de los héroes y de los sabios, el poeta hace su invocación a Apolo-

El diagrama de Gafurius podría relacionarse con la visión bíblica como una caída, el exilio de Eva, sometida al tiempo y las tentaciones. Y de igual modo las Musas y las Artes estarían condenadas, como dicta el Primer Mandamiento bíblico contra las imágenes. Esto se contrapone en gran medida a la interpretación clásico-pagana, donde la serpiente no estaría en oposición al dios, sino que es una manifestación de su fuerza y armonía, que debe superar las etapas del Mundo y del Tiempo para trascender, a través de la Iniciación, al don de la Inmortalidad. Son éstas afirmaciones que coinciden con la doctrina gnóstica.

 El monocordio

El monocordio, con su sistema de relaciones y proporciones, también fue representado. Pitágoras (siglo VI adC) hizo famoso este instrumento que utilizó para identificar y definir los intervalos musicales y en la enseñanza de la teoría pitagórica de la relación entre los números y la música; entre otras cosas demostró que la frecuencia del sonido es inversamente proporcional a la longitud de la cuerda.

En un grabado del siglo XVI atribuido al filosofo inglés L Fudd, C = Do = 384 Hz.se indica:

Que los puntos A y B del triangulo isósceles son asociados con la idea de α (principio) y ω (fin), lo que facilitó asumir la teoría de las proporciones a la vez que la relacionaba con uno de los atributos de Dios, Dios es el principio y el fin.

Afinado

Dado que el instrumento solo dispone de una cuerda, el afinado consiste en aplicar a la cuerda una tensión que produzca la nota deseada de la escala.

En el Diapasón, una vez fijada la nota base, desplazando el soporte deslizante según los intervalos definidos por Pitá se pueden fijar distintas longitudes de cuerda cada una con diferente nota desde los tonos bajos a los altos.

Existe una ilustración egipcia que concuerda ampliamente en su significado con el grabado de Gafurius.

El dios de las nueve cabezas está de pie sobre un cocodrilo con cabeza de halcón, y la representación entera está rodeada por una serpiente que se muerde la cola.



“Tú, que reinas en la tierra y en el agua, que sacudes al mundo, ser de lascola. Al pie se encuentran las siete vocales del alfabeto griego, que simbolizan los siete planetas del sistema ptolemaico; la serpiente muestra que el principio y el fin se encuentran, que “el uno y el todo” (en kaipan) concurren La serpiente también simboliza la eternidad (Eón), El dios de nueve cabezas es el dios-Sol, como se colige de otro texto, en el que se le llama Amo del Mundo:

“Nueve cabezas, coronado por nubes negras, quien traspasas el éter”.

Éste es el dios-Sol egipcio, que atraviesa los cielos en su barca, traspasando el éter húmedo. Sus nueve formas significan su infinita capacidad de transformación. El tres es el plural egipcio, y nueve es tres veces tres, el plural de plurales, el Infinito.

El cocodrilo simboliza a la vez el elemento agua y el tiempo mismo, como se puede observar en pasajes de Clemente de Alejandría y de Porfirio. La figura del dios de nueve cabezas sobre el cocodrilo representa al dios-Sol en su barca, cruzando el mar celeste y creando el tiempo.

En una segunda versión, Noun representa las aguas primordiales de las que emergen los dos brazos de Non, símbolo del paso de Uno a Dos, de donde procede la creación, representada por la barca del día en la que el escarabajo empuja al globo solar delante de él. En el grabado se ve a Nout, el Cielo, que recibe el Sol. Está de pie sobre la cabeza de Osiris quien rodea con su propio cuerpo la Douat (el mundo invertido).En la barca, Hou, el Verbo creador y Sia, el conocimiento, llevan el timón.



Fuente:http://minervaserranocantero.wordpress.com/matematicas-y-geometria/